پروژه روش عناصر مرزی - تفاضلات متناهی برای معادلات پواسون روی شبکه مثلثی با استفاده از نرم افزار MATLAB

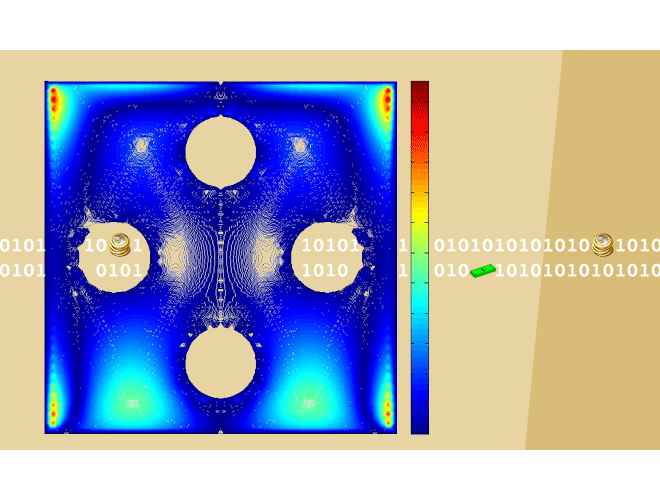
آنچه در این برنامه ارائه گردیده است حل معادلات پواسون با شرایط مرزی دریکله در نواحی دو بعدی شامل حفره، با استفاده از نرم افزار MATLAB ( متلب ) می‌‌باشد. نوع روش عددی در این برنامه، ترکیبی از روش تفاضلات متناهی با روش عنصر مرزی می‌باشد. با این روش مسئله را با تقریب خطی قطعه‌‌ای و یک دستگاه خطی پراکنده با وجود استفاده از عنصرهای مرزی حل می‌کنیم. مرزهای در نظر گرفته شده در این مسئله مستطیل‌‌هایی با حفره‌‌های دایره‌‌ای یا مستطیلی می‌‌باشند. تقسیم‌بندی ناحیه به صورت مثلثی در یک برنامه به صورت جدا انجام می‌‌شود که در این برنامه به صورت پیش فرض قرار داده شده است. با توجه به اینکه برای تقسیم‌بندی ناحیه از شبکه‌‌های تقریبی مثلثی استفاده می‌‌شود لذا میتوان این برنامه را برای حل مسائل پواسون به نواحی با مرزهای متنوع‌تری تعمیم داد. همگرایی این روش نسبت به اندازه طول مثلث‌‌های مقسم، از مرتبه دوم می‌باشد. سرعت این برنامه برای حل مسئله نسبت به دقت حل آن و ناحیه مورد نظر قابل توجه می‌باشد.

آنچه در این کد خواهید آموخت:

1- نحوه تبدیل مسائل مقدار مرزی به دستگاه‌های معادل با وزن‌های مشخص با استفاده از عملگرهای تفاضلی تقریبی

2- نحوه تولید شبکه با سلول‌های مثلثی منعطف با نواحی مختلف حفره دار

3- نحوه اندیس گذاری نقاط گره‌ای جهت اعمال محاسبات

4- نحوه ذخیره جداگانه نواحی شبکه بندی شده با تعداد نقاط گره‌ای متفاوت مرزی و داخل

5- نحوه پیاده سازی سه روش برای نقاط گره‌ای اندیس گذاری شده شبکه به صورت جامع برای هر تابع دلخواه روی مرز و تابع دلخواه منبع

6- محاسبه خطاهای مختلف از سه روش تقریبی به کار گرفته شده با استفاده از نرم افزار MATLAB ( متلب )

نکات و الزامات:

1- این برنامه در همه نسخه های کامپایلرهای نرم افزار MATLAB ( متلب ) قابل اجرا است

2- خروجی ها به فرمت‌های .m، .fig و .mat قابل مشاهده است

3- آشنایی اولیه با مفاهیمی مانند Boundary Value Problem, Delaunay Triangulation

4- آشنایی با Finite Difference Methods, Boundary Element Method

5- آشنایی با زبان Matlab

ریاضی
حوزه تخصصی 1	حل معادلات
مشخصات کلی
تعداد صفحات	34
تعداد صفحات محصول	20-40
معرفی متغیر های ورودی نرم افزار	دارد
نمودارهای خروجی	دارد
زبان برنامه نویسی
زبان برنامه نویسی اول	MATLAB

نظر بدهید

نام شما

نظر شما

توجه: HTML ترجمه نمی شود!

رتبه بد خوب

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Aliquam iaculis egestas laoreet. Etiam faucibus massa sed risus lacinia in vulputate dolor imperdiet. Curabitur pharetra, purus a commodo dignissim, sapien nulla tempus nisi, et varius nulla urna at arcu.Lorem ipsum dolor sit amet, consectetur adipiscing elit. Aliquam iaculis egestas laoreet. Etiam faucibus massa sed risus lacinia in vulputate dolor imperdiet. Curabitur pharetra, purus a commodo dignissim, sapien nulla tempus nisi, et varius nulla urna at arcuLorem ipsum dolor sit amet, consectetur adipiscing elit. Aliquam iaculis egestas laoreet. Etiam faucibus massa sed risus lacinia in vulputate dolor imperdiet. Curabitur pharetra, purus a commodo dignissim, sapien nulla tempus nisi, et varius nulla urna at arcu.