-
سبد خرید شما خالی است!
عالی عالی

بار بحرانی فشاری و بار بحرانی کمانش در ستونها و صفحه ها
در ادامه مقالات آموزشی مربوط به رشته مهندسی مکانیک گرایش جامدات در این مقاله به آشنایی با بار بحرانی فشاری و بار بحرانی کمانش در ستونها و صفحه ها می پردازیم که امیدواریم برای دانشجویان کارشناسی ارشد برای تولید مقالات علمی و پژوهشی و ارایه پایان نامه های کارشناسی ارشد مفید واقع شود . در ادامه این مقاله آموزشی به آشنایی با بار بحرانی در ستون ها می پردازیم .
مقدار بار بحران ، بیشترین مقدار باری است که یک ستون می تواند تحمل کند تا زمانی که حالت ابتدایی و مستقیم خود را حفظ کند . مقدار این بار به وسیلهی رابطهی زیر مشخص میگردد .
که در آن :
P : بار بحرانی (بار فشاری در جهت طولی در ستونها)
E : مدول الاستیسیته مادهای که ستون از آن ساخته شده
I : ممان اینرسی سطح مقطع تیر
L : طول تیر
K : ضریب طول موثر ستون
فرمول (1-1) در سال 1757 توسط ریاضیدان سوئیسی اولر ارائه گردد .
که K برای حالتهای مختلف ، متفات است که در جدول (1-1) شرایط مختلف و همچنین مقادیر K برای هر کدام از آنها آورده شده است . که خط پر حالت ابتدایی ستون را نشان می دهد و حالت خطچین حالت ستون را پس از کمانش بیان می کند .
جدول (1-1) شرایط و حالات مختلف ستون و ضریب
![]()
به بار بحرانی حاصل از رابطهی (1-1) بار بحرانی کمانش نیز اطلاق میشود یعنی بار کمانش بیشترین مقدار باری است که یک ستون می تواند تحمل کند تا دچار ازکار افتادگی و انحراف جانبی نگردد .
ستونها برای بارهای کمتر از بار بحرانی به صورت مستقیم و بدون کمانش باقی می مانند . بار بحرانی بیشترین باری است که ستون می تواند تحمل کند تا دچار انحراف جانبی (کمانش) نشود . برای بارهای بیشتر از بار بحرانی ، ستون انحراف جانبی پیدا میکند . بار بحرانی ، ستون را در یک شرایط ناپایدار تعادلی قرار می دهد که مقدار کمی بار بیشتر از مقدار بحرانی می تواند باعث واماندگی و از کارافتادگی ستون به وسیلهی کمانش گردد .
همچنان که بار از مقدار بار بحرانی بیشتر می شود میزان انحراف جانبی ستون نیز افزایش می یابد تا اینکه ستون در شرایط مختلفی مانند رسیدن به حد تسلیم ماده دچار شکست و از کار افتادگی گردد .
فرضیات زیر برای بیان فرمول اولر وجود دارند :
در شکل (1) تنش بحرانی در برابر نسبت لاغری برای ماده فولاد با مدول الاستیسیته E=200GPa و تنش تسلیم 240MPa رسم شده است که همانگونه که مشاهده می شود در قسمت رنگی ، از بعد از نسبت لاغری 89 ، ستون دچار کمانش می گردد . و در مقادیر کمتر از نسبت لاغری 89، تنش از مقدار تنش تسلیم فولاد بیشتر میشود که در این قسمت ماده تسلیم میگردد .
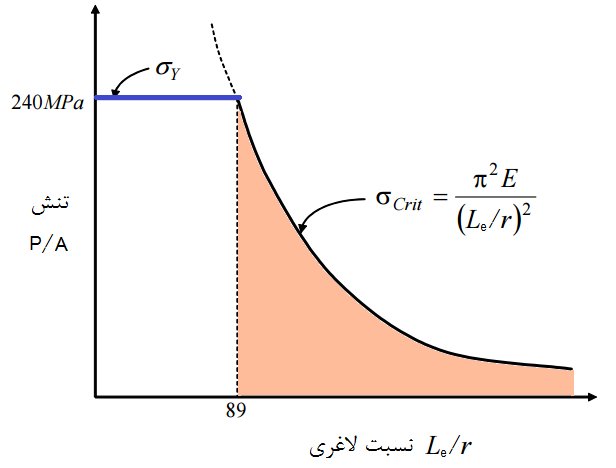
شکل (1-1) تنش بحرانی در برابر نسبت لاغری برای ماده فولاد
فرمول اولر را برای بارهای کمتر از تنش تسلیم ماده به صورت رابطهی (1-2) نیز بیان می کنند .
که در آن :
L/r : ضریب لاغری
L : طول موثر
r : شعاع ژیراسیون
A : مساحت سطح مقطع
I : ممان اینرسی
در ادامه این مقاله آموزشی به آشنایی با انواع کمانش پرداخته می شود .
از لحاظ ساختار مواد سازنده ، میتوان دو نوع کمانش الاستیک و غیر الاستیک را متصور شد . در کمانش الاستیک فرض میشود منحنی تنش-کرنش ماده خطی است ، یا به عبارتی روابط از قانون هوک پیروی میکند . در این حالت تنشها مقادیر کمتر از تنش تسلیم را اختیار میکنند و برای مدول الاستیسیته میتوان مقدار ثابتی در نظر گرفت . در کمانش غیر الاستیک با افزایش میزان تنشها از میزان تنش تسلیم مصالح سازنده ، منحنی تنش-کرنش غیرخطی خواهد بود ، لذا مقدار مدول الاستیسیته متناسب با تنش اعمالشده تغییر خواهد کرد . در این حالت در گسترش معادلات دیفرانسیل حاکم باید دقت بیشتری نمود .
علاوه بر کمانش الاستیک و غیر الاستیک، بهطورکلی در سازههای تحت بار فشاری امکان رخ دادن سه نوع کمانش وجود دارد :
در کمانش جانبی که اغلب مربوط به تیرها و ستونها هست ، بدون اینکه تغییر شکلی در مقطع عضو رخ دهد ، سازه دچار تغییر مکان جانبی میشود . در این حالت مقطع در طول خود انحنا مییابد (شکل 1-2 الف) در کمانش موضعی ، مقطع عضو سازهای انحنا مییابد . (شکل 1-2 ب) کمانش واپیچشی به ترکیبی از دو نوع کمانش فوق اطلاق میگردد. (شکل 1-2 ج)
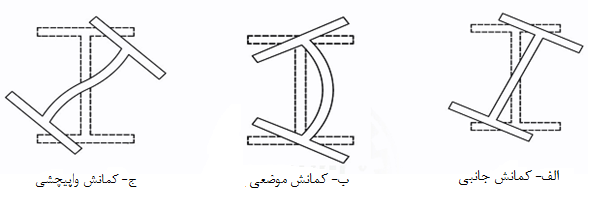
بررسی انواع کمانش
در قسمت قبل به بررسی بار کمانش بحرانی برای ستونها و تیرها پرداختیم در این قسمت به بررسی کمانش ورقها و صفحه ها تحت بارگذاری فشاری درون صفحه خواهیم پرداخت .
2-1-کمانش ورق
صفحات نازک در سازههایی چون صنایع هوانوردی و کشتیسازی به کار میروند ، اغلب در معرض بارهای درون صفحه فشاری و نیروهای برشی در صفحه ورق عمل میکنند قرار میگیرند . (شکل 2-1) . اگر این نیروها کوچک باشند ، هیچگونه تغییر مکان خارج از صفحه در ورق ایجاد نمیشود ( w=0 , u=o , v=0 ) . در این حالت گوییم ورق در حالت تعادل پایدار است .
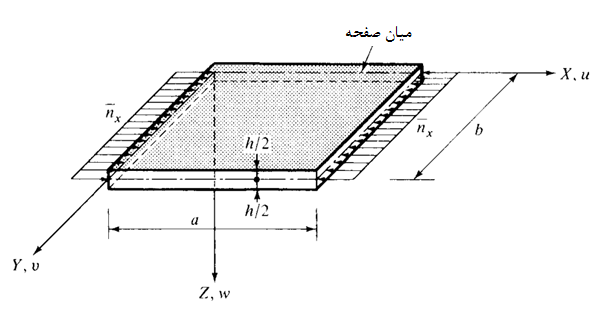
شکل 2-1 صفحه مستطیلی تحت بار درون صفحه فشاری
درصورتیکه بارگذاری ادامه پیدا کند، در مقدار مشخصی از بار در روند تغییر شکل ورق بهطور ناگهانی تغییر رخ میدهد . تغییر شکل خارج از صفحه ورق همزمان با تغییر شکل درون صفحه ورق اتفاق میافتد . به این پدیده کمانش ورق میگویند . باری که در آن کمانش رخ میدهد ، بهعنوان بار بحرانی معرفی میشود . اهمیت بار بحرانی ازآنجهت است که با افزایش میزان آن ، تغییر شکلهای خارجی بسیار بزرگ در ورق رخ میدهد ، که در نهایت منجر به گسیختگی کامل ورق خواهد شد . شرایط فوق بسیار خطرناک است و در طراحی سازهها باید از به وقوع پیوستن چنین شرایطی جلوگیری کرد .
مفهوم کمانش ورق با بیان مثال بسیار ساده حالتهای مختلف تعادل یک گوی صلب قابللمس خواهد بود . اگر گوی در یک مکان مقعر قرار گیرد (شکل 2-2-حالت الف) اصطلاحاً در حالت تعادل پایدار است . اگر با ایجاد یک تغییر مکان کوچک بهاندازه x در گوی، تعادل آن به هم بخورد ، پس از چند نوسان ، گوی به مکان اول خود بازمیگردد . اگر گوی روی مکان مسطحی باشد (شکل 2-2-حالت ب) در حالت تعادل خنثی قرار دارد ، به این معنا که با اعمال تغییر مکان کوچک x تعادل نیرویی آن برهم نمیخورد و در انرژی پتانسیل آن تغییری به وجود نمیآید . اگر گوی بر روی یک سطح محدب قرار گیرد(شکل 2-2-حالت ج) بهاصطلاح در حالت تعادل ناپایدار است . در این صورت ، اعمال تغییر مکان کوچک x باعث برهم خوردن تعادل گوی و ناپایداری آن میشود . ذکر این نکته بسیار مهم است که در تئوری کلاسیک ورق همواره در مسیر تغییر وضعیت یک سیستم از حالت تعادل پایدار و رسیدن به حالت ناپایدار ، تعادل خنثی رخ میدهد .
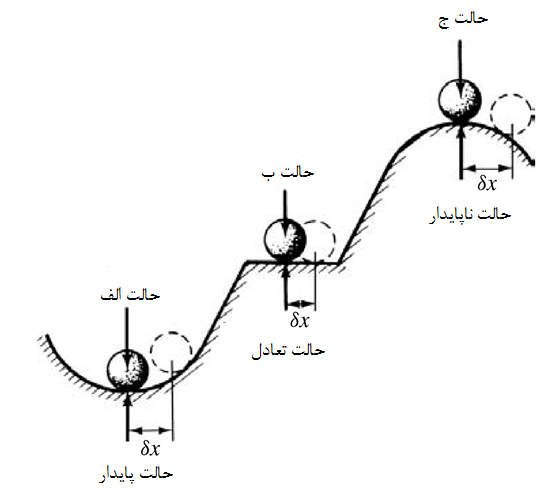
شکل (2-2) بررسی شرایط مختلف پایداری
تمامی فرمولبندیهای تحلیل مسائل الاستیک خطی مربوط به پایداری ورق بر مبنای این فرضیه شکلگرفتهاند . باوجودی که یک ورق دارای درجات آزادی نامحدودی است ، با توجه به مسئله کمانش ورق از تعداد درجات آزادی کمتری میتوان استفاده کرد .
در فرمولبندی مسائل الاستیک پایداری ، حالت تعادل پایدار بهعنوان نقطه دوشاخهای شدن معرفی میگردد . با رسیدن بار به میزان بحرانی ، از دو مسیر ممکن تغییر شکل (یکی مربوط به تعادل پایدار و دیگری در ارتباط با تعادل ناپایدار) ورق همواره دچار کمانش میشود (شکل 2-3) . علاوه برفرض وجود نقطهی دوشاخهای شدن ، در تحلیل پایداری الاستیک ورق فرض میکنیم قانون هوک معتبر است .
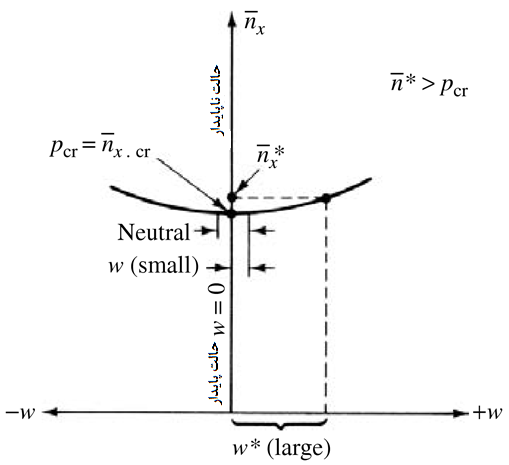
شکل (2-3) نمودار دوشاخهای شدن
علاوه بر نظریه کلاسیک کمانش ورق ، رفتار ورقها بعد از کمانش نیز حائز اهمیت هست . تحلیل فرا کمانش ورقها به دلیل غیرخطی بودن ، یکی از مسائل بسیار پیچیده است . نوع دیگری از رفتار کمانشی مربوط به ورقهای دارای انحنای کم هست . چنین ورقهایی هرگاه بهصورت همزمان در معرض بارهای فشاری درون صفحه و بارهای جانبی قرار گیرند ، رفتاری به نام کمانش سراسری ناگهانی از خود بروز میدهند . ویژگی این رفتار تغییر شکل معکوس ورق به دلیل رابطه غیرخطی بین بار کمانش و تغییر شکل است . در طول یک فرآیند بارگذاری پیوسته و رسیدن بهی ک بار بحرانی ناگهان ورق در جهتی مخالف جهت قبل ، کمانش مییابد .
در این مقاله آموزشی سعی بر آموزش مقدماتی و آشنایی دانشجویان کارشناسی ارشد با مبحث کمانش شده است تا بتوانند با استفاده از آن به ارایه پایان نامه های کارشناسی ارشد , تولید مقالات علمی و پژوهشی بپردازند .
بسیاری از پروژه های و مسایل مربوط به کمانش بوسیله نرم افزار های مهندسی matlab و ABAQUS حل می گردد .
نرم افزار های Matlab و ABAQUS از مهم ترین نرم افزار های مهندسی در رشته های مختلفی هم چون مهندسی مکانیک , برق و عمران می باشند که در در بسیاری از پایان نامه های کارشناسی ارشد , پروژه های علمی , پژوهشی و صنعتی کاربرد دارند .
برای آشنایی با نرم افزار های Matlab و ABAQUS هم چنین آموزش نصب نرم افزار های Matlab و ABAQUS می توانید بر روی نام این دو نرم افزار کلیک نمایید تا به مقاله های مورد نظر منتقل شوید .
برای استفاده از پروژه های مربوط به کمانش می توانید با کلیک بر روی محصولات مرتبط به صفحه مربوط به محصولات مربوطه منتقل شوید .
برای مطالعه مقالات علمی بیشتر می توانید مقالات زیر را مشاهده نمایید :
مدل سازی توربو ماشین در نرم افزار Fluent
م