پروژه نرم افزار بهینه‌سازی گرادیانی مقید با استفاده از نرم افزارهای فرترن و ++C

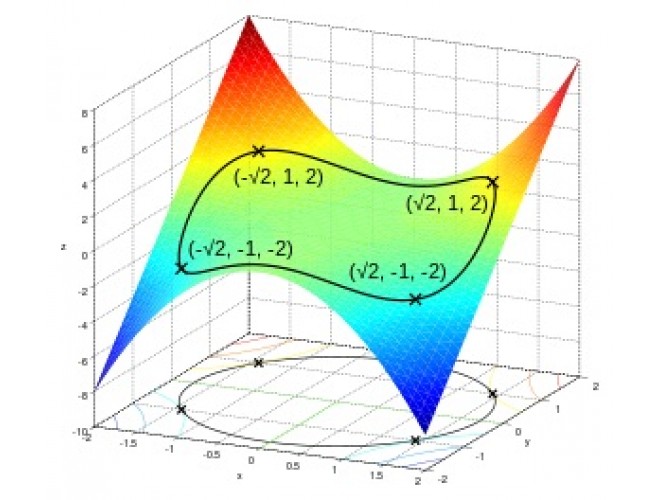
آنچه در این برنامه ارایه گردیده است توسعه کد بهینه‌سازی بر مبنای روش‌های گرادیانی مقید می‌باشد. در این برنامه از پنج روش شناخته شده گرادیانی مقید به نام‌های روش پنالتی داخلی، روش پنالتی خارجی، روش ضرایب لاگرانژ تکمیل شده، روش برنامه‌نویسی خطی متوالی و روش برنامه‌نویسی مرتبه دوم متوالی که در ادامه به توضیح آنها می‌پردازیم استفاده شده است. در این گزارش ابتدا پنج روش فوق و همچنین بقیه الزامات این روش‌ها را به اختصار توضیح داده و سپس برای اعتبار سنجی از چند نمونه تابع ریاضی به همراه قیدهای مساوی و یا نامساوی استفاده شده است. روش‌های گرادیانی مقید بر مبنای گرادیان تابع هزینه و قیود مسئله کار می‌کنند. این روش‌ها برای نقض نکردن قیود مسئله از متدهای مختلفی استفاده می‌کنند و در مقایسه با روشهای گرادیانی نا مقید دارای هزینه محاسباتی بیشتری می‌باشند. در این گونه روش‌ها نیز یکی از مشکلات اساسی این است که ممکن است به جای بدست آوردن نقطه بیشینه یا کمینه سراسری، در نقطه اکسترمم محلی متوقف شوند.

آنچه در این کد خواهیم آموخت:

۱- حل مسائل بهینه‌سازی مقید

۲- اعمال روش‌های بهینه‌سازی مقید به مسئله بهینه‌سازی

۳- معادلات و الگوریتم روشهای بهینه‌سازی مقید

۴- نحوه محاسبه توابع پنالتی و لاگرانژ

۵- نحوه خطی‌سازی مسئله بهینه‌سازی

۶- روش SIMPLEX

۷- نحوه مینیمم سازی توابع هزینه ریاضی با حل مسئله بهینه سازی

ریاضی
حوزه تخصصی 1	سایر
مشخصات کلی
تعداد صفحات	41
تعداد صفحات محصول	40-60
معرفی متغیر های ورودی نرم افزار	دارد
نمودارهای خروجی	دارد
زبان برنامه نویسی
زبان برنامه نویسی اول	FORTRAN
زبان برنامه نویسی دوم	++C

نظر بدهید

نام شما

نظر شما

توجه: HTML ترجمه نمی شود!

رتبه بد خوب

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Aliquam iaculis egestas laoreet. Etiam faucibus massa sed risus lacinia in vulputate dolor imperdiet. Curabitur pharetra, purus a commodo dignissim, sapien nulla tempus nisi, et varius nulla urna at arcu.Lorem ipsum dolor sit amet, consectetur adipiscing elit. Aliquam iaculis egestas laoreet. Etiam faucibus massa sed risus lacinia in vulputate dolor imperdiet. Curabitur pharetra, purus a commodo dignissim, sapien nulla tempus nisi, et varius nulla urna at arcuLorem ipsum dolor sit amet, consectetur adipiscing elit. Aliquam iaculis egestas laoreet. Etiam faucibus massa sed risus lacinia in vulputate dolor imperdiet. Curabitur pharetra, purus a commodo dignissim, sapien nulla tempus nisi, et varius nulla urna at arcu.